地球流体セミナー/
講演資料一覧/
2002-03-25 /
カオス的混合と輸送障壁
水田 亮 (京都大学大学院理学研究科地球惑星科学専攻)
[email protected]
2002 年 3 月 26 日
講演ビデオを見るには, 以下の各スライド画像をクリックし,
左上に表示される「ビデオ開始」をクリックしてください.
講演資料

|
目次
|

|
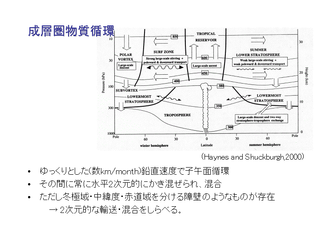
- 流れが周期的, 規則的であっても混合の様子が予測不可能.
- 「乱流混合」と区別する.
|

|
どこがカオスか?
- 2 次元非発散の流れを表す流線関数は
ハミルトン力学の表現形式と対応がつく.
|

|
カオス的な流れの例: ベナール対流
定常な流れ (右上図) に周期的な微小摂動が加わったとすると…
- (オイラー的な)流れ場は予測できる
- 粒子の混合の様子は予測できない. カオス的に混ざる.
下図は流体粒子混合の時間発展.
|

|
カオス的な流れの例: 管の中の流れ
|
|
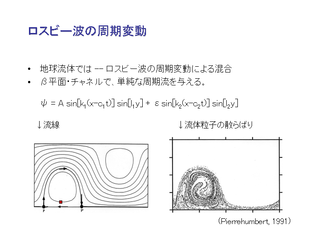
ロスビー波の周期変動
- ジェットの両側に混合領域が現れる.
- 混合領域内部に孤立した混合の少ない領域が現れる.
|

|
よどみ点の存在が鍵となる.
流脈線: 点源からトレーサを放出し続けた際のある時刻のトレーサの分布と解釈できる
homoclinic orbit: よどみ点が一つ (左図)
- Wu(P) はよどみ点 P
近傍から流れた流体粒子の流脈線.
- Ws(P) はよどみ点 P
近傍へ向かう流体粒子の流脈線.
- 交点はよどみ点近傍から流れ出て, よどみ点近傍に再び戻る点.
- 交点で囲まれた領域 A は 周期とともに A', A'' へと移動する.
|

|
heteroclinic orbit: よどみ点が二つ以上 (右図)
例: シアー流中のキャッツアイ構造
- 一方のよどみ点がもう一方のよどみ点に対し周期的に時間変動すると,
時間変動するよどみ点の周囲で「おりたたみ」と「引き延ばし」が発生し,
効率のよい混合が発生する.
- よどみ点がないと「おりたたみ」と「引き延ばし」が生じない.
|
|
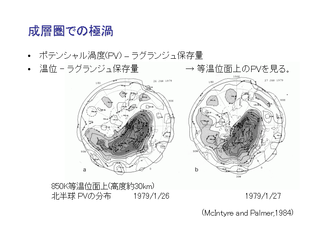
成層圏でのポテンシャル渦度(PV)分布
PV のコンターが流されて, 細くなり, ちぎれていく.
|

|
極渦と輸送障壁
- 初期にジェットを囲むコンターを置く.
- 数周期後には複雑に混合される.
- ジェットの外側には微細な構造が生じる.
|
|
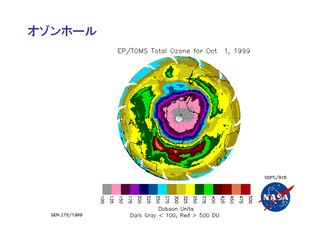
オゾンホール
|

|
観測される微細構造
|

|
問題意識
|

|
数値モデル
|

|
粒子移流の計算手順
|
|
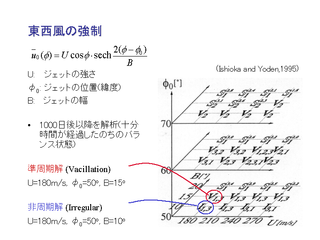
東西風の強制
- ジェット中心の緯度, 風速, ジェットの幅をパラメータとする.
- 十分時間が経過すると, パラメータによって 3 種類の状態が現れる.
|

|
準周期解と非周期解におけるジェットの南北分布
|

|
計算結果: 準周期解
|

|
ジェットを境にして赤と青の粒子は混ざらない.
|

|
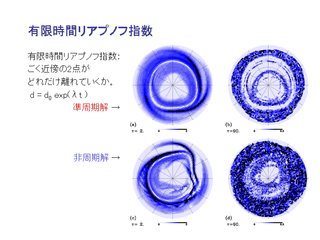
有限時間リアプノフ指数の導入
実際の計算では…
- ある程度引き伸ばされた時点で変移を縮小する.
これによって面積の有限な球面上でも事実上無限に計算できる.
|
|
有限時間リアプノフ指数からわかること
- 赤と青の粒子で埋められた領域のリアプノフ指数は,
90 日程度でそれなりに一様になる.
- 先の粒子混合実験結果は初期位置の選択によらないことが示唆される.
- 中心領域内にはさらに細かい構造が見える.
- 異なる場所を初期位置にして粒子混合実験結果を再度行うと,
同様のパターンが現れることが期待される.
|
|
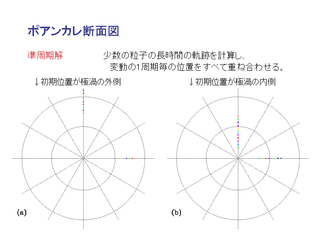
ポアンカレ断面
ある流体粒子の初期値と周期毎の位置を重ね合わせて表示したもの.
|

|
ポアンカレ断面 (1000 周期後)
- いろいろな時刻における粒子位置の重ねあわせ.
- 有限リアプノフ指数よりも細かい構造が見える.
|
|
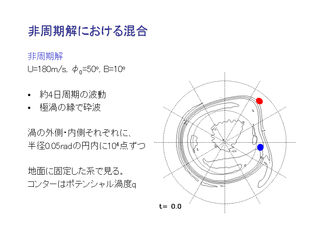
非周期解の場合の混合
|

|
流体粒子の分布を示している.
相関次元
- D 〜 1 の場合, 線状な分布
- D 〜 2 の場合, 面状な分布
- 初期値は面的な分布.
- 初めは線的な分布, 大きなスケールから次第に面的な分布になる.
拡散などでは小さいスケールから面的な分布になる.
|

|
孤立領域に粒子をおいてさらに 90 日計算
- |トーラスではない|
- 中心の茶色はほとんど動かない,
- 緑, 赤は, ポアンカレマップにおける中心領域の三組の斑点においてある.
それぞれ三組の斑点領域を一周期毎に移動するが混ざらない.
|
|
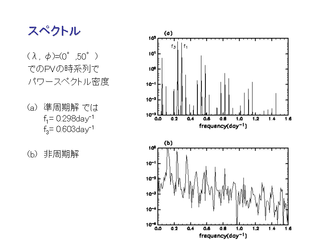
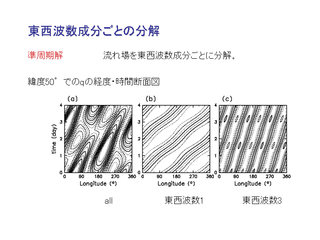
波数分解
|
|
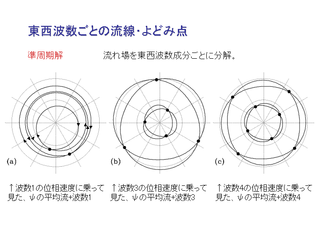
流線と淀み点 (hyperbolic point) の分布
それぞれ, 平均流と波数成分での淀み点と流脈線を示している.
ポアンカレ断面図における
- 外部領域の三日月と内部領域の三日月は平均流 + 波数 1
- 内部領域の三組の斑点は平均流 + 波数 3
と対応する.
|

|
β面モデルとの比較
- 三日月状のパターン分布の位相は, β面と球面とで異なる.
|

|
まとめ
|
- Andrews, D. G., J. R. Holton, and C. B. Leovy, 1987:
Middle Atmosphere Dynamics.
Academic Press, 489pp.
- Aref, H., 1984:
Stirring by chaotic advection.
J. Fluid Mech., 143, 1-21.
- Chen, P., 1994:
The permeability of the Antarctic vortex edge.
J. Geophys. Res., 99, 20563-20571.
- Haynes, P. H., 1989:
The effect of barotropic instability on the nonlinear evolution
of a Rossby-wave critical layer.
J. Fluid Mech., 207, 231-266.
- Haynes, P. H. , and E. F. Shuckburgh, 2000:
Effective diffusivity as a diagnostic of atmospheric transport.
1. Stratosphere.
J. Geophys. Res., 105, 22777-22794.
- Ishioka, K., and S. Yoden, 1995:
Non-linear aspects of a barotropically unstable polar vortex
in a forced-dissipative system: Flow regimes and tracer transport.
J. Meteor. Soc. Japan, 73, 201-212.
- Malhotra, N., and S. Wiggins, 1998:
Geometric structures, lobe dynamics, and Lagrangian transport
in flows with aperiodic time-dependence,
with applications to Rossby wave flow.
J. Nonlinear Sci., 8, 401-456.
- McIntyre, M. E., and T. N. Palmer, 1984:
The ``surf zone'' in the stratosphere.
J. Atmos. Terr. Phys., 46, 825-849.
- Neufeld, Z., C. Lopez,
E. Hernandez-Garcia, and T. Tel, 2000:
Multifractal structure of chaotically advected chemical fields.
Phys. Rev., E 61, 3857--3866.
- Ottino, J. M., 1989:
The Kinematics of Mixing: Stretching, Chaos, and Transport.
Cambridge University Press, 364pp.
- Pierrehumbert, R. T., 1991:
Chaotic mixing of tracer and vorticity by modulated travelling Rossby waves.
Geophys. Astrophys. Fluid Dyn., 58, 285-319.
- Polvani, L. M., and R. A. Plumb, 1992:
Rossby wave breaking, microbreaking, filamentation, and secondary vortex
formation: The dynamics of a perturbed vortex.
J. Atmos. Sci., 49, 462-476.
- Tuck, A. F., 1989:
Synoptic and chemical evolution of the Antarctic vortex in late winter and
early spring, 1987.
J. Geophys. Res., 94, 11687-11737.
|
Odaka Masatsugu & Sasaki Youhei
2003-09-03
|